—Vamos, Ven —dijo Sal —. Estoy deseando llegar para prepararnos la merienda.
—Voy todo lo rápido que puedo, Sal —respondió el pequeño —, pero es que estas manzanas pesan mucho.
—No te quejes, enano —dijo el gafotas —, que yo llevo todo el queso…
—Claro, como te has comprado todo el queso del super… —protestó el pequeño — Oye, Sal, ¿te puedo hacer una pregunta?
—Dime.
—¿¿Cuánto te has gastado en queso?? —le espetó Ven un poco ofuscado.
—No tanto… —respondió este —¿Por qué?
—Porque mamá te avisó de que no te pasaras comprando queso, ¿sabes?
—Bueno —se defendió el mayor —, mamá nos dio 20 € y nos han sobrado 4. No lo hemos gastado todo y hemos comprado también manzanas y pan.
—Ya, pero las manzanas y el pan eran más baratas —insistía Ven en su reprimenda.
—No te creas —siguió el gafotas —, en manzanas hemos gastado el doble que en pan.
—¿Y en queso? —continuó el pequeño en su indagación.
—En queso sólo el triple que en pan —dijo Sal y añadió bajando la voz —más lo que hemos gastado en manzanas.
—¿Y eso cuánto es? —preguntó Ven cada vez más impaciente.
—Huy, eso se puede calcular muy bien resolviendo un sistema de ecuaciones —intervino Mati que había estado pendiente de la conversación mientras los acompañaba de vuelta a casa.
—Ea, pues ya sabes, Ven —concluyó el gafotas —, solo tienes que resolver el sistema de ecuaciones que dice Mati.
—¿Qué ecuaciones, Mati? ..preguntó el pequeño —¿Cuál es la incógnita?
—Las, las incógnitas —dijo esta —. Son tres en este caso: lo que habéis gastado en manzanas, lo que habéis gastado en pan y lo que habéis gastado en queso.
—¿¿3 incógnitas?? —el gafotas se interesó de pronto en la conversación —Solo sabemos resolver sistemas de 2 ecuaciones con 2 incógnitas.
—Sí —confirmó Mati —, pero el mismo método de Gauss que os enseñé para sistemas de 2 ecuaciones con 2 incógnitas se puede usar para sistemas de 3 ecuaciones con 3 incógnitas.
—¿Seguro? —preguntó Sal desconfiado —¿Cómo?
—Os lo explico con vuestra compra —les dijo Mati —. Vamos a definir las incógnitas del problema.
—Esto tiene pinta de ser muy difícil… —dijo Ven por lo bajini.
—Para nada, Ven —dijo ella —, ya verás. Ahora vamos a ir escribiendo las ecuaciones con los datos que me habéis dicho ¿Cuánto habéis gastado en total?
—¡16 €! —se apresuró a contestar el pequeño.
—Ajá, eso significa que la suma de las 3 incógnitas es igual a 16.
—En manzanas hemos gastado el doble que en pan —añadió el gafotas.
—Muy bien —dijo la pelirroja —, vamos a expresar ese dato como otra ecuación:
—Sí, pero en queso hemos gastado el triple que en pan más lo que hemos gastado en manzanas —dijo Ven con vehemencia.
—Ese dato —dijo Mati —lo expresaremos de la siguiente forma:
—¿3 ecuaciones? —preguntó Ven con cara de espanto.
—Sí —le respondió Mati —. Si queremos tener un solución única, necesitamos, al menos, tantas ecuaciones como incógnitas, como nos pasaba el otro día. Ya tenemos nuestro sistema de ecuaciones:
—¿Y ahora? —preguntó impaciente el gafotas.
—Ahora —les dijo —ordenamos la escena del crimen, poniendo todas las incógnitas en el término de la izquierda:
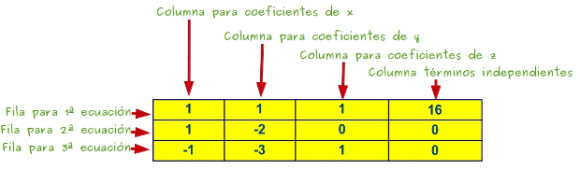
—¿Ahora tenemos que escribir la cajita de coeficientes, Mati? —preguntó Sal.
—Efectivamente —confirmo esta —.Vamos a escribir la matriz de coeficientes:
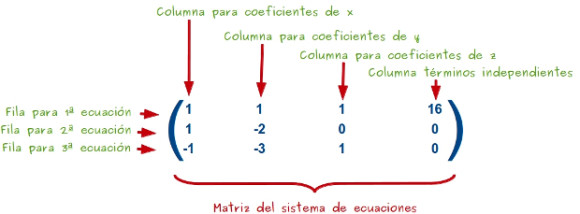
—Ahora —continuó Mati —la escribimos como nos gusta a los matemáticos…
—¿Qué hacemos ahora, Mati? —preguntó el pequeño.
—Lo que tenemos que conseguir operando con las filas —dijo ella —es transformar en 0 los números que os marco con círculos en la matriz:
—Empezamos con el número del círculo rojo —propuso Mati —. Como es un 1 igual que el mismo número en su posición en la Fila 1, sólo tenemos que calcular Fila 2 menos la Fila 1, y sustituir la Fila 2 por la nueva fila obtenida:
—Con esto, la matriz de coeficientes se transforma en la siguiente: -dijo la pelirroja.
—Le toca el turno —anunció ella —al número en el círculo verde. Como es -1 y en la Fila 1 en esa columna tenemos un 1, bastará con sumar la Fila 3 con la Fila 1, y sustituir la Fila 3 por la nueva fila obtenida.
—Sustituimos en la matriz de coeficientes —continuó Mati —la Fila 3 por la nueva fila obtenida
—¡Eh, el número del círculo amarillo ha cambiado! —exclamó Ven.
—Efectivamente —dijo Mati —si hubiese cambiado a 0 ya habríamos acabado. Pero no, aún no es 0. Tenemos que seguir currando. Pero antes que nada, fijaos que todos los coeficientes de la Fila 3 son pares, todos son divisibles por 2.
—Ajá —dijeron los dos hermanos al unísono.
—Cuando toda una fila es divisible por un número -dijo Mati —podemos dividir la fila por ese número en cuestión y así trabajaremos con números más pequeños.
—¡Mola! -dijo Ven, Sal lo miró muy serio.
—Si dividimos la Fila 3 por 2, nos quedará:
—Otra vez ha cambiado el número del círculo amarillo, Mati —advirtió el pequeño.
—Sí, pero sigue sin ser 0 —respondió Mati —. Para conseguir que el -1 en el círculo amarillo sea 0, ahora usamos la Fila 2, porque si usamos la Fila 1 podríamos perder el 0 del círculo verde que acabamos de conseguir.
—Ajá —repitió Ven, Sal esta vez no lo miró.
—Tenemos que multiplicar el número de la Fila 2 correspondiente a la columna de nuestro círculo amarillo, el -3 en nuestro ejemplo, por un número para que el resultado sea 1 y al sumarlo a la Fila 3, nuestro -1 se convierta en un 0.
—Eso es imposible —dijo Ven.
—¿Por qué? —preguntó ella.
—Ningún número multiplicado por -3 da como resultado 1 —dijo el pequeño.
—Eso no es verdad —intervino el gafotas —Si multiplicas -1/3 por -3, el resultado es 1.
—Ajá —dijo de nuevo Ven rascándose la barbilla. Gauss resopló,
—Muy bien, chicos —continuó Mati —. Multiplicaremos la Fila 2 por -1/3 y lo sumaremos a la Fila 3, el resultado será la nueva Fila 3 de la matriz de coeficientes.
—Ahora tenemos la matriz:
—Mati —dijo Sal —¿podemos multiplicar la última fila por 3 para quitar los denominadores?
—Podemos —confirmó ella.
—Pero ahora —dijo Ven excitado —¡se puede dividir la Fila 3 por 4!
—Ajá —dijo Mati cómica —, podemos.
—Ya no podemos hacer nada más —se lamentó Ven.
—Bueno —dijo Mati —, vamos a escribir el sistema de ecuaciones asociado a esta matriz y ya veréis que fácil es resolverlo:
—¡Toma, toma, toma! ¡Cómo mola! —gritó el pequeñajo —Ya sabemos que z vale 10 —Ven hizo un pausa —¿¿Te has gastado 10 € en queso??
—No es tanto, Ven —se defendió el gafotas —, es un queso francés y estaba en oferta.
—¿Cuánto hemos gastado en pan, chicos? —preguntó Mati tratando de desviar la conversación —Podéis calcularlo muy fácilmente con la segunda ecuación, sustituyendo z por 10.
Los niños se pusieron a calcular lo que Mati había propuesto.
—Hemos gastado 2 € en pan, Mati —anunció Ven.
—Y como en total hemos gastado 16 € —añadió su hermano —, hemos gastado 4 € en manzanas.
—¡Muy bien, chicos! —exclamó Mati con alegría —. Ya os dije que el método de Gauss también servía para 3 ecuaciones, y para 4, para 5…
—¡¡Gaussito es el mejor!! —gritó Ven tomando a su mascota en brazos.
—Lo es —apostilló el gafotas —, pero vamos ya a casa que quiero mi bocata de queso.










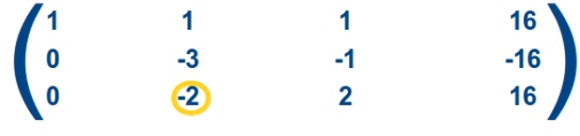





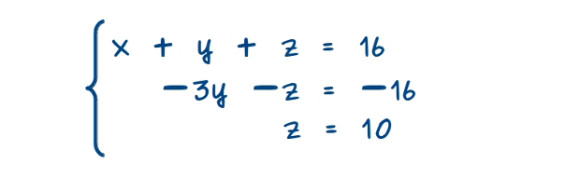

Existe la posibilidad de que «huy», renglón 19, sea sin «h». Claro que con «h» es aún más sorprendente, como ¡más metida en su papel!. Poesía pura…
Como siempre la «clase» es una delicia:
Vivan Mati, Gauss y Sal
vivan Ven , Clara y Raquel
que saben entretener
con manzanas, queso y pan
mejor que nadie. Así es.
El cálculo matricial es una maravilla, por su potencia y su sencillez. ¡Qué buenos y dilatados ratos he pasado con la resolución (o deconvolución) de curvas (con mi propio programa en lenguaje C) basado en el algoritmo de Meiron. Con dos curvas no había problemas obteniendo fielmente las curvas «originales» (mezcla de Gauss-Cauchy) solapantes con cuya suma o envolvente trabajaba; un mayor número de ellas me obligaba a tocar el factor de amortiguamiento y hacer otras «perrerías»… La ciencia es hermosa y las matemáticas son el peine perfumado que la acicala, que pone todo en su sitio…que etiqueta y pone precio a todo.
2 veces mas en manzanas que en pan….
3 veces mas en queso que en pan….
pan=x, manzanas=2x, queso=3x
Sin duda Gauss fue uno de los mejores matemáticos de la historia, si no el mejor aunque fuera de los circuitos matemáticos no se le reconoce lo suficiente. Un genio.
Mierda de blog . adeu .. Andreu
@moe, y el mejor científico Maxwell.