Anteriormente en Mati, una profesora muy particular…
En el capítulo de hoy…
—¿Has terminado tus deberes, Sal?
—Casi. Me falta muy, muy poco.
—¡Bien! Ahora podemos ir a jugar al parque.
—No, voy a esperar a Mati que está a punto de llegar. Quiero que me enseñe a hacer raíces cuadradas.
—Jo, pero eso debe ser muy complicado, gafotas…
—¿Qué es lo que debe ser muy complicado para estos dos niños tan listos? —Mati acababa de entrar.
—¡Hola, Mati! —saludó Sal efusivamente.
—Hola, Mati, —saludó el pequeño Ven — Calcular raíces cuadradas. Yo sólo estoy en segundo…
—Bueno, pero te voy a enseñar un método para hacerlo en el que sólo se necesita saber sumar, multiplicar y dividir. Y como Sal está en 5º y ya sabe hacerlo…
El gafotas sonrió orgulloso.
—¿Sólo con eso? —preguntó Sal.
—Sólo con eso, caballeros —afirmó Mati —¿Queréis que os lo cuente?
—¡Sí! —respondieron al unísono los dos hermanos.
—A ver, decidme un número… —dijo la pelirroja.
—Pero, Mati, ¿qué significa la raíz cuadrada? —preguntó Ven arrugando mucho la naricilla.
—La raíz cuadrada de un número es otro número de forma que si éste lo multiplicamos por sí mismo, nos sale el primero —respondió ella.
Ante la cara de desconcierto del pequeño Ven, Mati continuó:
—Por ejemplo, la raíz cuadrada de 4 es 2, porque 2 x 2 es 4, ¿me explico?
—Entiendo… —dijo Ven pensativo —O sea que la raíz cuadrada de 9 es 3, porque 3 x 3 es 9, ¿no es así?
—Efectivamente, muy bien, Ven.
—¿Nos podemos ir ya al parque?
—No, Ven —protestó su hermano — Ésas son las fáciles —y dirigiéndose a Mati dijo —Quiero calcular la raíz cuadrada de … de 247.
—Toma… —se asombró el pequeño.
—Muy bien —dijo Mati— Decidme un número que creáis que podría ser la raíz cuadrada de 247.
Sal se puso a pensar, Ven puso la mano en el hombro de su hermano mostrando apoyo moral.
—Bueno… —pensaba el gafotas —10 x 10 son 100…es muy poco…20 x 20 son 400 eso es mucho …15 x 15 es… 15 x 10 que son 150 más 15 x 5 que son 5 x 5 x 3…75… O sea, 225… Es poco, también…
—Sí, pero está cerca de 247 —dijo Mati— Empecemos con 15, por ejemplo. podemos empezar con cualquier número que multiplicado por sí mismo dé menos que 247.
Mati tomó su libreta.
—Ahora nos preguntamos, ¿es 15 la raíz cuadrada de 247? Si no sabemos cuánto es 15 x 15, para comprobar si 15 es la raíz cuadrada de 247, dividimos 247 entre 15. Si no sale 15, es que no es su raíz cuadrada.
—¿Puedo hacer yo la división, Mati? —preguntó Sal.
—¡Claro!
Sal se puso a trabajar en la libreta.
—¿Cuántos decimales saco?
—Nos conformaremos con 3.
—De todas formas, ya sé que todos los demás serán 6... -añadió Sal.
—Ahora hacemos lo siguiente: como nuestro primer candidato, 15, no era la raíz cuadrada de 247, nos fijamos en el resultado de dividir 247 entre 15, que es 16’466. Hacemos las media entre el primer candidato y el resultado de esta división, y tendremos el segundo candidato a ser la raíz cuadrada de 247 : 15’733.
—¿Y ahora, Mati? —preguntó Sal impaciente.
—Vamos a hacer lo mismo. Dividimos 247 entre el segundo candidato, 15’733, para ver si es su raíz cuadrada, si no nos sale el segundo candidato, hacemos la media entre él y el resultado de la división para obtener el tercer candidato. Lo vamos a escribir en una tabla para que se vea más claro el proceso.
—Y ahora, Mati, dividimos 247 entre el tercer candidato, que es 15’716, a ver si nos sale lo mismo, ¿no? —preguntó el gafotas.
—Eso es —respondió ella.
—¡Toma, toma, toma! ¡Cómo mola! ¡Ya nos ha salido! —el pequeño Ven no supo disimular su emoción.
—La raíz cuadrada de 247 es 15’716 —dijo Sal con voz de presentador de televisión.
—Sí, señor. Si queréis obtener más cifras decimales, basta con obtener más decimales desde el principio de este proceso.
—¡Qué fácil, Mati! —Sal estaba entusiamado.
—Sí, este método permite fácil y rápidamente calcular la raíz cuadrada de un número y es más fácil de recordar que el que me contaron a mí cuando iba al cole —respondió la pelirroja.
—¿Cómo era? —quiso saber Sal.
—Al final, no iremos al parque… -se quejó su hermano.
—Veréis hacíamos un dibujo como éste. Separábamos las cifras de 2 en 2, empezando por la derecha y nos fijábamos en las 2 que se quedaban más a la izquierda. En este caso sólo una, el 2. Ahora pensamos qué número al cuadrado, es decir, multiplicado por sí mismo, da 2 o menos de 2, que es la cifra que estamos mirando.
—¡El 1! —dijo Sal inmediatamente.
—Muy bien, Sal. Ése lo ponemos ya arriba en naranja, porque es definitivo. Ahora restamos 1, a 2 y bajamos las dos cifras siguientes. tenemos el 147. Separamos la cifra de la derecha, el 7, y nos fijamos en 14.
—En otro nivel, que marcamos con otra línea, multiplicamos 2 por el número que está arriba ya definitivo, el que hemos puesto en color naranja. En nuestro caso, 2 x 1, que es 2. Tenemos que conseguir un número A de forma que 2A x A, sea menor que 147. Probamos con A igual a 7, que es el número que hemos separado, 14, dividido por 2, que hemos obtenido de 2 x 1.
—No, vale, Mati —dijo Ven —Sale 189.
—Probemos con A igual a 6…
—Tampoco vale —protestó el pequeño — Sale 156.
—A ver con A igual a 5…
—¡Toma, éste sí! —contestó ven con alegría —Es 125, menor que 147.
—Muy bien, Ven. Subimos el 5 arriba, lo ponemos en naranja, porque es definitivo. Restamos 125 de 147 y para poder calcular decimales, como no nos quedan más números, bajamos dos ceros y repetimos el proceso —continuó Mati — Separamos el 0 de la derecha de 2200, nos quedan 220. Multiplicamos 2 por la cifra naranja, 15, nos da 30 y necesitamos un número A de forma que 30A x A sea menor que 2200. probamos con 220 dividido entre 30, o sea , 7, y sí, sale. Subimos el 7 arriba, en naranja.
—Es un poco lío, Mati… —se quejó Ven.
—Sí, el primero era más fácil —corroboró Sal.
—Efectivamente —dijo ella —y todavía sólo hemos sacado un decimal, si queremos 3, como antes, tendremos que seguir añadiendo ceros de 2 en 2.
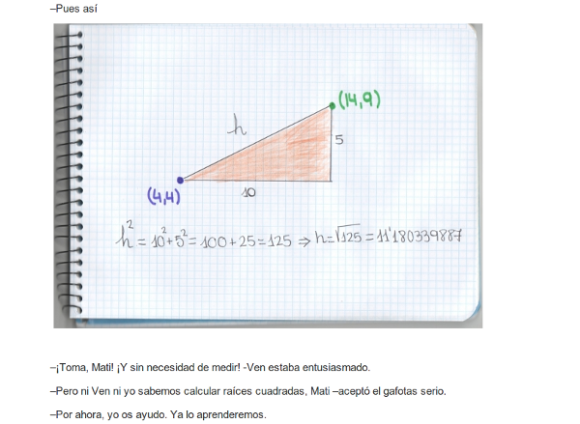
—Pues yo me quedaré con el primero para calcular las distancias con el teorema de Pitágoras —concluyó Sal.
—¿Y si hablamos de esto en el parque? —preguntó Ven con una sonrisa pícara.
—Yo creo que sí —respondió la gafotas —Este perrito necesita un poco de aire fresco…
A lo mejor Gauss no estaba tan equivocado con los de sus raíces cuadradas, mirad si no cómo son los árboles que rodean la facultad de Matemáticas de la Universidad de Sevilla… 😉

- Foto de Zifra












Como siempre muy buena la pedagogía. Es fundamental acercar las mates a los más pequeños para que dejen de ver en ellas un ogro.
Nunca se me han dado bien las raíces cuadradas, hasta que tuve mi primera calculadora. Desde entonces, desde aquel maravilloso día, no se me han dado ni bien, ni mal. No se me han dado en absoluto. Con apretar el botón, salían instantáneamente y con una precisión pasmosa.
Tengo casi 47 años, y pese a que reconozco que es una de mis asignaturas pendientes, no me apetece recuperarla ahora, aunque los dos métodos explicados, y la forma en la que están explicados, lo pone bastante fácil.
Peor es la raiz cubica y que cierren tantisimas empresas dejando en el paro a tanta muchedumbre ¿No?
Hoy Mati nos trae un método (iterativo) para calcular la raíz cuadrada de un número.
Independientemente de la necesidad o no de aprender a calcular la raíz cuadrada de un número a mano, que yo, sinceramente no acabo de verla si no se explica el ‘funcionamiento interno’ del algoritmo (y eso no se hace), este método es mucho más simple para explicar en primaria que el método que, al menos, me explicaron a mí. Mati también cuenta aquel método en el post.
Pues eso, ahí tenéis los dos: el segundo de ellos por si os viene bien que os lo recuerden para ayudar a vuestros hijos con las tareas, el primero para que se lo enseñéis como método alternativo más fácil y operativo 😉
Gracias por los comentarios.
Clara
Hola Mati!
Acabo de recordar cómo hacer raíces cuadradas sin la calculadora gracias a ti! Y de una forma mucho más fácil de como me lo enseñaron (lo 2º que has explicado).
Te visitaré a menudo porque seguro que me serás muy útil cuando mis hijos me pregunten jejeje
Sólo un apunte, si me lo permites: lo de «gafotas» suena muy despectivo, no resulta en absoluto agradable ni cariñoso, que supongo que es lo que se pretende…
Saludos
Es el algoritmo de Newton-Rapson.
Efectivamente 🙂
os superáis de entrega a entrega, ésta me encanta…. gracias por hacer que las matemáticas sean sencillas, comprensibles y…. divertidas…..
😉
Es una forma genial de explicar y entender las raíces cuadradas! Hace muchoo tiempo que las aprendí porque no tenía otra en el cole, por quinto puede ser?, y me parecieron lo más feo que había en las matemáticas, después llegó la calculadora y me vino genial. Ahora con mi peque, que le quedan unos cuántos años para llegar a quinto de primaria, me viene muy bien anotarme estas ideas, no sólo por poderle enseñar cuando lo necesite sino también por mí, recordarlo y no verlo tan mal..
Gracias por mostrar las mates desde un punto de vista tan práctico, útil y divertido.
Como estudiante de matemáticas: ¡¡GRACIAS!! (¡el día menos pensado cuando diga que estudio mates me miran con la misma cara que si digo que estudio derecho! 😉 )
Lo que hacéis ya es bonito, pero ¡cómo lo hacéis! es fantástico. Mi más sincera enhorabuena.
Y lo siento El Principe Malko, las raíces cuadradas se te siguen dando mal, sólo que sabes mandar a otro, en este caso una calculadora, que te las haga. Pero supongo que como a casi todo el mundo confundes hacer matemáticas con los cálculos, que es una mínima parte de lo que las matemáticas son.
Iba a poner un testamento sobre las utilidades, y lo relativas que ellas son, pero sólo diré que nunca ha habido un buen jefe que no sepa hacer el trabajo de un empleado. Comprender por qué se hace así y por qué se puede hacer así, por qué funciona va mucho más allá de saber mandarle a una calculadora que te calcule la raíz cuadrada de 0.00000004.
¡Un saludo a todos!
Arizona
Hablando de raíces cuadradas,en este enlace escribí unos versos que me enseñó una compañera sobre la raíz cuadrada:
http://catedu.es/matryc/index.php?option=com_content&view=article&id=116:raiz-cuadrada&catid=47:en-el-lenguaje&Itemid=76
Aunque haya alguna palabra local, se entiende. Espero que os guste.