—¿Jugamos al Hex un rato, Sal?
—No puedo, Ven, tengo que hacer la tarea de Mates.
—¿Te queda mucho?
—No, solo unas sumas de fracciones.
—¿Me enseñas a sumar fracciones? —pidió Ven a su hermano.
—Toma, calcula esto que es muy fácil.
El pequeño Ven se dispuso alegremente a realizar la suma que le había propuesto su hermano, 3/5 más 2/5…
—¡Hala, qué burro! Pero, ¿qué has hecho, Ven? —preguntó el gafotas exaltado.
—No me llames burro, tú –se quejó el pequeño reprimiendo un puchero –. Estoy en 3º y aún no hemos estudiado las sumas de fracciones…
—Lo siento, Ven –dijo Sal mientras le ponía un brazo por los hombros –Se me ha escapado… Te enseñaré cómo se hace, ¿quieres?
—Bueno, bueno, bueno… —Mati acababa de llegar – ¿Jugando a profesor y alumno?
—¡Hola, Mati! —saludaron los dos pequeños, Gauss ladró.
—Iba a enseñarle a Ven a sumar fracciones –añadió Sal.
Mati miró lo que había escrito Ven y dijo:
—Ah, ya veo… pero cuando los denominadores son iguales, sólo tenemos que sumar los numeradores, Ven.
—Es que en su clase aún no han explicado fracciones, Mati –se apresuró a excusarlo su hermano.
—Eso –añadió Ven.
—Ya, ya, lo sé –dijo ella –Debes pensar en las fracciones como si fueran trozos de tarta, ya verás cómo es más fácil…
—¿Trozos de tarta? —preguntó el pequeño rápidamente.
—Sí –respondió Mati –. Si dividimos una tarta en 5 trozos, 1/5 será un trozo, 2/5 serán dos trozos, 3/5 serán 3… Ahora piensa, ¿cuánto son 3/5 más 2/5?
—¡Cinco trozos! —exclamó Ven.
—Eso es –dijo Sal con una enorme sonrisa –. Serían 5/5, o lo que es lo mismo, 1, porque sería la tarta entera.
—Muy bien, chicos –añadió la pelirroja.
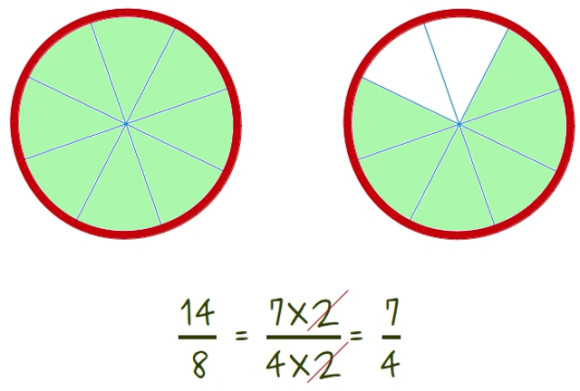
—Ahora lo comprendo todo –dijo Ven ceremonioso –Así que solo sumamos los números de arriba… 3/8 más 11/8 serán 14 /8… ¡Eh! Un momento, no pueden ser 14/8. Eso es más de una tarta.
—Cierto –confirmó la pelirroja y añadió guiñando un ojo–. Pero nadie dijo que solo tuviésemos una tarta. Además, fíjate, Ven, que 14 es 7 por 2 y 8 es 4 por 2, podemos, en ese caso, eliminar ese 2 en el numerador y el denominador y nos queda una fracción más elegante.
—¡Toma! ¡Claro! —aceptó un Ven entusiasmado, pero su cara perdió de pronto el color —¿Qué pasa si no son iguales los denominadores, Mati?
—Vamos a pensarlo, ¿no? —propuso ella –Imaginemos que tenemos que sumar 3/8 + 1/6… Lo dibujamos como porciones de tarta
—Ahora nos fijamos en la suma –les dijo –. No podemos hablar de octavos, porque el trozo resultante de sumar tiene un lado azul (el que representa los cortes en octavos) y otro en verde (que representa los cortes en sextos, en 6 partes iguales). Por la misma razón, no podemos hablar de sextos, ¿no?
—Claaaaaaaaro –murmuró Ven.
—¿Qué podemos hacer, chicos? —les preguntó Mati.
—Hacer porciones de distinto tamaño, ¿no? Más pequeñas –propuso Sal.
—Efectivamente –dijo ella –. En nuestras dos tartas iniciales, vamos a hacer nuevos cortes para dividir en fracciones de forma que al superponerlas, al sumarlas, las líneas azules y las líneas verdes coincidan. Para ello, el número de trozos debe ser el mismo en ambas tartas, ¿no?
—Ajá –asintió Ven muy teatrero.
—Tenemos que cortar cada uno de los 8 trozos de la primera tarta en un número N de trozos que nos darán en total 8xN porciones –les contó – y cada uno de los 6 trozos de la segunda tarta en M trozos, y nos quedarán 6xM porciones. Pero queremos que 8xN y 6xM sean iguales. Ahora bien, 8xN es un múltiplo de 8 y 6xM es un múltiplo de 6, por lo tanto necesitamos…
—¡Un múltiplo común a 6 y 8! —exclamó Sal.
—Eso es, muy bien –confirmó Mati –. Y para hacer el menor número de cortes, buscaremos…
—¡El mínimo común múltiplo! —gritó Ven con entusiasmo.
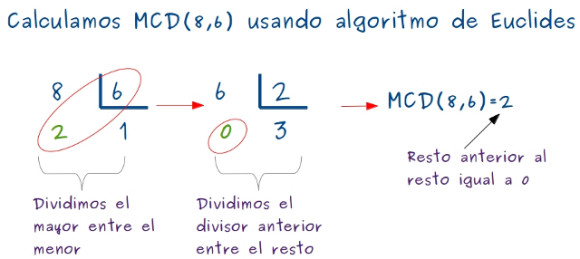
—Pero, bueno, ¡sois fantásticos! —la pelirroja estaba orgullosa, Gauss gruñó con pelusilla –Lo calculamos como os enseñé.
—Primero el máximo común denominador –propuso Sal.
—Y ahora dividimos 8 x 6 entre el MCD (8, 6) –concluyó el pequeño –y nos queda 24.
—Ya lo tenemos –anunció ella –Vamos a dividir cada tarta en 24 trozos. Para ello, cada trozo de la primera, lo cortamos en 3, 24/8, y cada trozo de la segunda, lo cortamos en 4, 24/6. Así tenemos que 3/8 son lo mismo que 9/24 y que 1/6 serán 4/24 y por lo tanto:
—¡13/24! ¡Toma, toma, toma! ¡Cómo mola! —gritó el pequeño.
—Pues ya lo sabes –concluyó la gafotas –Para sumar fracciones con distinto denominador, también nos sirve el mínimo común múltiplo del que hablamos el otro día.
—¿Me pones una suma, Mati? —pidió Ven y Mati le escribió una en su libreta: 8/15 + 5/6.
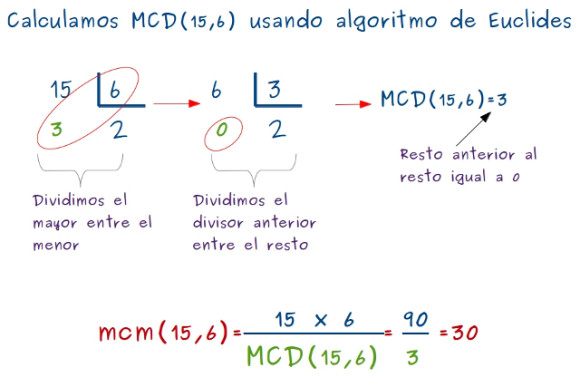
—Primero el mcm(15, 6) –dijo Sal y lo calcularon.
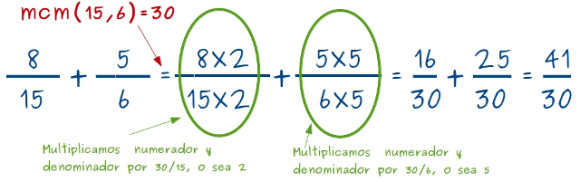
—Ahora tenemos que hacer 30 trozos de cada tarta –continuó el pequeño –O sea que en la de 15 trozos, hay que dividir cada trozo en 2 trozos, y por lo tanto, si 8/15 eran 15 trozos ahora tendré 16 trozos, es decir 16 trozos, que serán 16/30. En la tarta de 6 trozos, tengo que dividir cada uno de ellos en 5 trozos, por lo tanto, si 5/6 eran 5 trozos de esa tarta ahora tendré 5 por 5, 25 trozos de la nueva… 25/30. Y ahora 25 más 16… 41…¡41/30!
—Perfecto, Ven –le felicitó Mati–Ya sabes cómo sumar fracciones con distinto denominador –A continuación resumió todo el método en la libreta para que los chicos lo repasaran con ella.
—Pero, Mati –preguntó el gafotas —¿No es más rápido hacer la división que indica la fracción y luego sumar lo que nos sale?
—Bueno –dijo esta –, no siempre es más rápido, puesto que tienes que hacer la división y además, en la mayoría de los casos, no tendrás el resultado exacto. Por ejemplo, vamos a calcular 10/3 + 17/9. Si lo hacemos con el método que propones:
 —Pero si lo hacemos sumando las fracciones –continuó Mati –, que son los valores exactos de los números que queremos sumar:
—Pero si lo hacemos sumando las fracciones –continuó Mati –, que son los valores exactos de los números que queremos sumar:
—Como veis, el resultado es diferente –les dijo y añadió con sonrisa traviesa–. Es preferible tratar las fracciones como lo que son, fracciones, no tratar de ver sus intimidades que se pueden alterar los resultados y mis chicos son muy precisos en sus cálculos, ¿no?
—Totalmente –afirmó Ven con rotundidad.
—No lo había pensado –añadió el gafotas –. Prefiero hacerlo con fracciones, sí.
—Bueno, Sal –dijo de pronto el pequeño –, termina tu tarea, yo jugaré mientras con Mati al Hex, ¿vale?


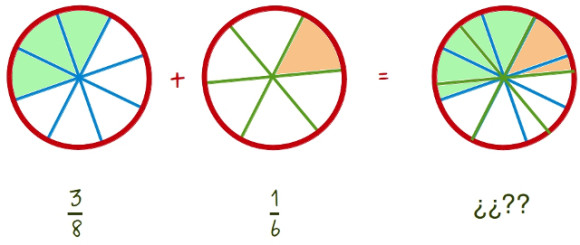
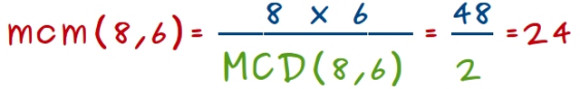


Una forma fácil y amena de aprender matemáticas
Qué bueno es tu blog. Me encanta!!
http://areaestudiantis.com/
Toda la vida soñando
con ser un número entero,
agua pura, azul del cielo,
algo sencillo y viajero,
buen futbolista, torero,
poeta, cantor y obrero,
que cuando ríe se ríe
y cuando llora es sincero,
y heme aquí que sólo soy
de ignorancias tesorero,
y el bien y el mal me acompañan
en este oscuro sendero
por las fracciones de España.