—Ya hemos llegado —dijo Ven —. Esta es la librería Voronoi.
—El que reparte el bacalao —bromeó Sal.
—¡Toma! ¡Cómo mola el escaparate con nuestro libro! —añadió el pequeño.
—¡Guauu, guauuuu!
—Sí, está precioso —dijo Mati —, me encanta.
—Y hemos llegado rapidísimo gracias al itinerario que tú has preparado, Mati —dijo el gafotas.
—Bueno, es que la Teoría de Grafos es muy apañada para diseñar rutas de recorridos mínimos —respondió ella con un guiño.
—¿Nos enseñas a hacerlo, Mati? —pidió Sal.
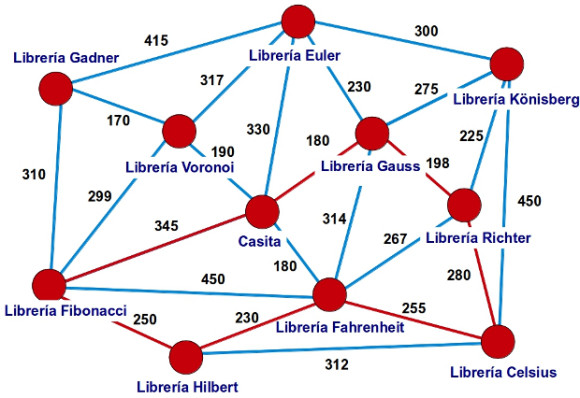
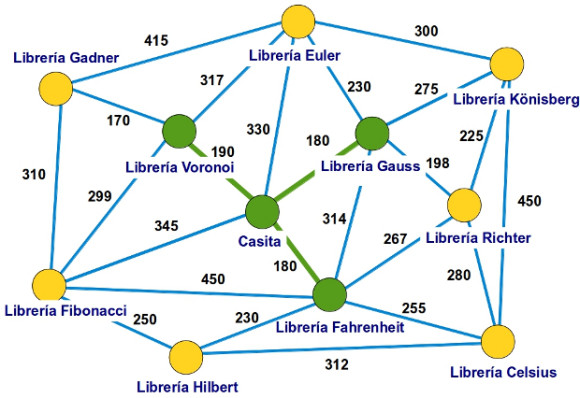
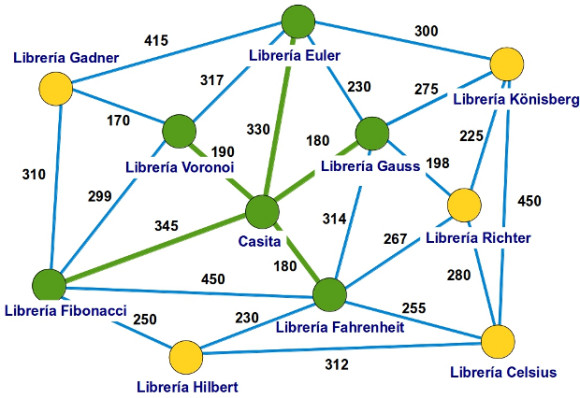
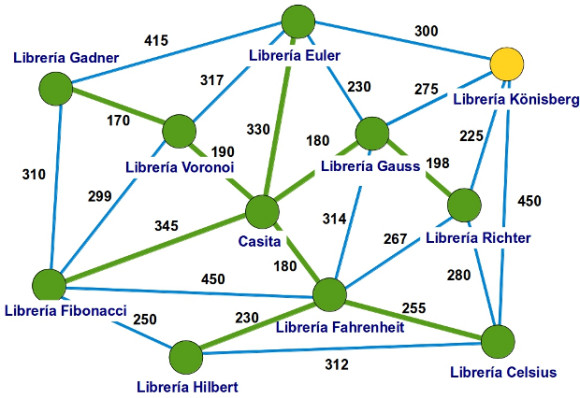
—Con muchísimo gusto —respondió la pelirroja —. Antes de planear la ruta, he dibujado un grafo de la siguiente manera: un vértice, un punto rojo, que representa a nuestra casita. Después he puesto un vértice por cada una de las 10 librerías que queríamos visitar hoy: Celsius, Euler, Fahrenheit, Fibonacci, Gadner, Gauss, Hilbert, Könisberg, Richter y Voronoi. A continuación, he dibujado aristas, segmentos azules, uniendo esas librerías indicando la distancia en metros de cada posible ruta que las unía, mirad:
—Vamos a construir los caminos de recorrido mínimo desde nuestra casita hasta cada una de las 10 librerías usando el algoritmo de Dijsktra —continuó Mati —El resultado de esta construcción será un árbol.
—¿Un árbol? —preguntó Ven con cara de sorpresa.
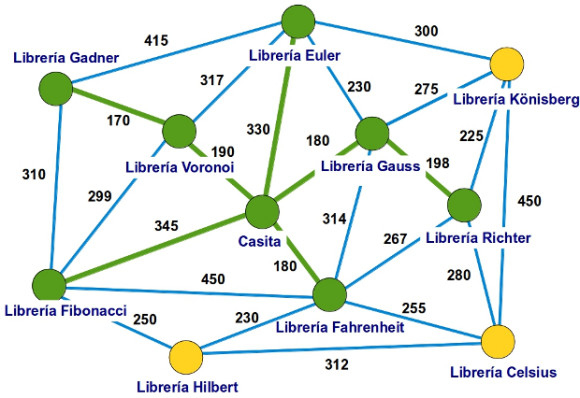
—Sí, un árbol —confirmó ella —Es decir, nos quedaremos solo con algunas de las aristas azules de este grafo que acabamos de dibujar de forma que todas las librerías aparecen conectadas con esas aristas y se puede ir de uno a cualquier otro paseando por ellas. Además, no se forman ciclos de aristas, es decir, no hay ningún recorrido circular como el que aparece marcado con trazo rojo en la siguiente imagen.
—¿Y cómo sabemos qué aristas se quedan y qué aristas se van?—preguntó el gafotas.
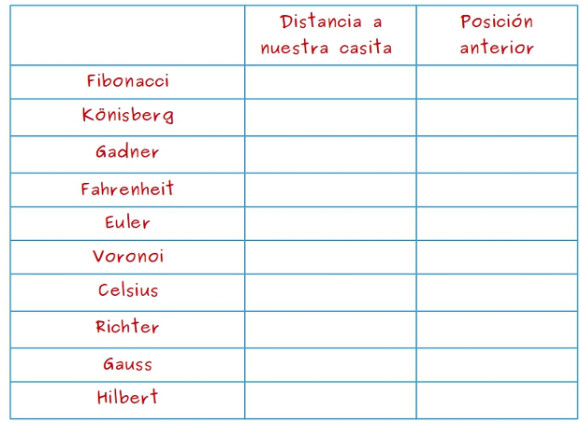
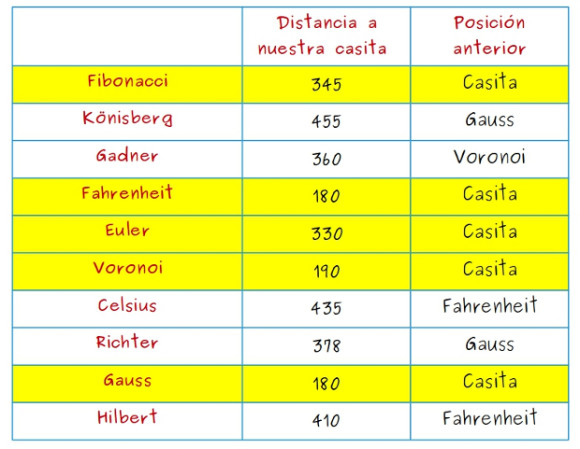
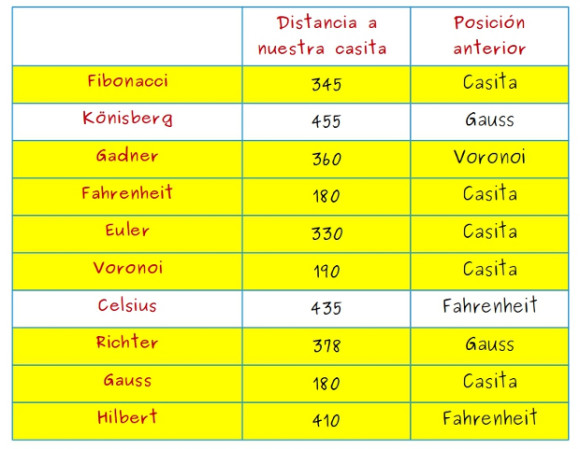
—Eso es lo que os voy a explicar ahora mismo —anunció Mati con una sonrisa —Para ello, vamos a hacer una tabla que nos ayude, como esta:
—En la primera columna —continuó ella —ponemos el nombre de las librerías que queremos visitar. En la columna central, escribimos la longitud del camino más corto desde casa a la librería correspondiente encontrado hasta ese momento, y en la última columna el nombre de la última librería de ese camino que hemos visitado antes de llegar a la librería de esa fila.
Los niños asintieron con la cabeza y permanecieron muy atentos, Gauss se dedicó a mirar a las perritas que pasaban…
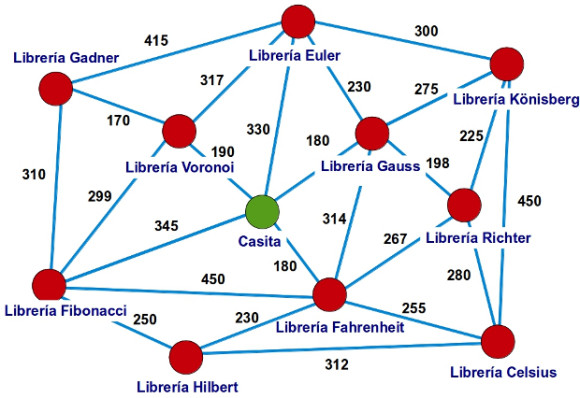
—Comenzamos desde el vértice que representa a nuestra casa —siguió la pelirroja —, ¿a cuántas librerías podemos llegar directamente desde Casita?
—A 5 —dijo Sal —: a la librerías Gauss, Euler, Voronoi, Fibonacci y Fahrenheit.
—Efectivamente —confirmó Mati —, vamos a pintar esas librerías de amarillo:
—Ahora miramos la distancia desde casa a cada una de esas 5 librerías —siguió ella —y la escribimos en la tabla, a las librerías que no están conectadas con nuestra casa le asignamos la distancia infinito, ∞, porque aún no podemos llegar a ellas. En esta primera tabla, la en la columna de la derecha solo puede estar nuestra casa porque salimos de allí.
—Nos fijamos ahora en la librería más cercana de las 5 conectadas a casa —les propuso Mati.
—Hay 2 —dijo Ven rápidamente —, Gauss y Fahrenheit.
—Tendremos que elegir una de ellas —dijo Mati, ¿cuál?
—¡¡Gauss!! —respondieron los niños al unísono.
—¡Guauuuuu, guauuuuu, guaauuuu! —dijo… bueno, ya sabéis quién.
—Muy bien, elegimos la librería Gauss. Pintamos de verde el vértice correspondiente y la arista que la une con nuestra casa.—continuó Mati —. Y ahora desde esta librería, podremos llegar a otras nuevas.
—¡Sí! —exclamó el pequeño — A Euler y a Könisberg.
—Las pintamos de amarillo —concluyó Mati.
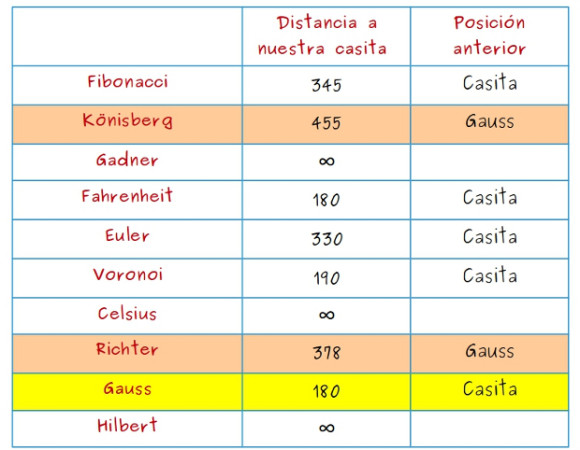
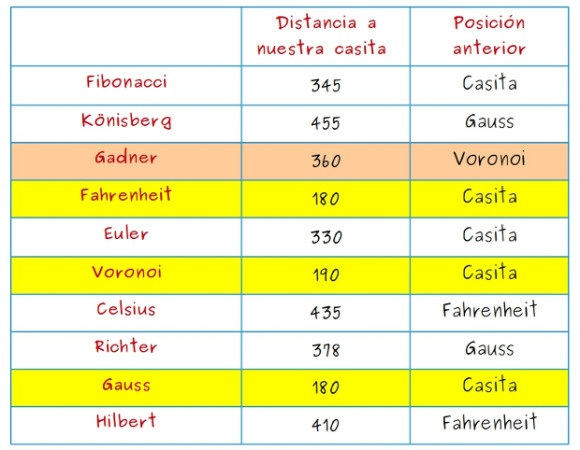
—A continuación, actualizamos la tabla —les dijo —. Desde la librería Gauss podemos llegar a Euler, Fahrenheit, Richter y Könisberg. Calcularemos el recorrido de los 4 caminos que, pasando por la librería Gauss, van de casa a cada una de estas 4 librerías, y para cada una de ellas nos quedamos con el que pasa por Gauss solo si es menor que el que ya está en la tabla. Para la librería Euler, el camino que pasa por Gauss mide 180 (arista entre Casita-Gauss) más 230 (arista Gauss-Euler), esto es, 410. Lo descartamos porque en la tabla anterior Euler está a 330 de casa. Para la librería Fahrenheit, el camino que pasa por Gauss mide 180 (arista entre Casita-Gauss) más 314 (arista Gauss-Fahrenheit), esto es, 494. Lo descartamos porque en la tabla anterior Fahrenheit está a 180 de casa. Para la librería Richter, el camino que pasa por Gauss mide 180 (arista entre Casita-Gauss) más 198 (arista Gauss-Richter), esto es, 378. Este sí lo cambiamos porque en la tabla anterior Richter estaba distancia infinita de casa. Y por último, para la librería Könisberg, el camino que pasa por Gauss mide 180 (arista entre Casita-Gauss) más 275 (arista Gauss-Könisberg), esto es, 455. Este también lo cambiamos porque en la tabla anterior Könisberg estaba distancia infinita de casa. Solo tenemos que actualizar Richter y Könisberg:
—Qué chulo, Mati… —Sal estaba embobado.
—Lo es —dijo ella —. Ahora miramos, de nuevo, la columna central y buscamos a quién corresponde el número más pequeño…
—¡Fahrenheit! —gritó Ven — ¡El de los termómetros de Estados Unidos!
—¡Vamos para allá! —exclamó Mati —¡Fahrenheit en verde!
—¡Ahora pillamos a Celsius y a Hilbert! —añadió el gafotas —¡Que se vuelvan amarillos!
—¡Toma, toma, toma! ¡Cómo mola! —dijo Ven.
—Actualicemos nuestra tabla —sugirió ella —Desde Fahrenheit se puede llegar a Richter, Celsius, Hilbert y Fibonacci. Estudiemos esos caminos: Para la librería Richter, el camino que pasa por Fahrenheit mide 180 (arista entre Casita-Fahrenheit) más 267 (arista Fahrenheit-Richter), esto es, 447. Lo descartamos porque en la tabla anterior Richter estaba a distancia 378 de casa. Para la librería Celsius, el camino que pasa por Fahrenheit mide 180 (arista entre Casita-Fahrenheit) más 255 (arista Fahrenheit-Celsius), esto es, 435. Este sí lo cambiamos porque en la tabla anterior Celsius estaba distancia infinita de casa. Para la librería Hilbert, el camino que pasa por Fahrenheit mide 180 (arista entre Casita-Fahrenheit) más 230(arista Fahrenheit-Hilbert), esto es, 410. Este también lo cambiamos porque en la tabla anterior Hilbert estaba distancia infinita de casa. Para la librería Fibonacci, el camino que pasa por Fahrenheit mide 180 (arista entre Casita-Fahrenheit) más 450 (arista Fahrenheit-Fibonacci), esto es, 630. Lo descartamos porque en la tabla anterior Fibonacci estaba a distancia 345 de casa. Solo cambiamos entonces Celsius y Hilbert:
—Como veis —dijo Mati —, estoy marcando en amarillo las librería que ya están en verde, porque esas ya están en nuestro árbol ¿Adónde vamos?
—¡A Voronoi! -gritaron los niños.
—Sí —dijo Mati —Desde Casita, como dice en la tabla. Pintamos de verde Voronoi y la arista que lo une con Casita.
—Y a Gadner de amarillo —añadió el gafotas —porque lo hemos pillado.
—¡Esto marcha! —dijo la gafotas —Vamos a actualizar la tabla —Desde Voronoi se puede llegar a Euler, Gadner y Fibonacci, veamos esas rutas. Para la librería Euler, el camino que pasa por Voronoi mide 190 (arista entre Casita-Voronoi) más 317 (arista Voronoi-Euler), esto es, 507. Lo descartamos porque en la tabla anterior Euler estaba a distancia 330 de casa. Para la librería Gadner, el camino que pasa por Voronoi mide 190 (arista entre Casita-Voronoi) más 170 (arista Voronoi-Gadner), esto es, 360. Este lo cambiamos porque en la tabla anterior Gadner estaba a distancia infinita de casa. Para la librería Fibonacci, el camino que pasa por Voronoi mide 190 (arista entre Casita-Voronoi) más 299 (arista Voronoi-Fibonacci), esto es, 489. Lo descartamos porque en la tabla anterior Fibonacci estaba a distancia 345 de casa. Solo cambiamos Gadner.
—¿Hacia dónde vamos, caballeros? —preguntó Mati.
—Hacia Euler —dijo el gafotas.
—El de los puentes de Könisberg —añadió Ven.
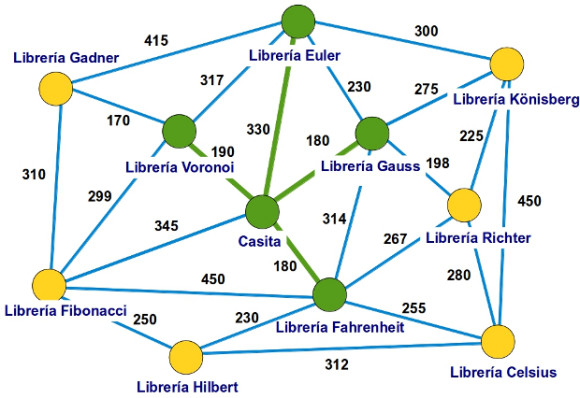
—Eso es —dijo ella —, vamos a Euler desde Casita según nuestra tabla. Pintamos de verde Euler y la arista Casita-Euler.
—Si miramos ahora las rutas que llegan a Gadner y a Könisberg pasando por Euler —continuó ella —, miden 745 y 630, respectivamente. son peores que las de la tabla que tenemos, así que no cambiamos nada. Y ahora, ¿adónde vamos?
—¡A Fibonacci! —dijo Sal.
—¡El de los conejos! —añadió su hermano.
—¡Allá vamos! —dijo Mati —¡A Fibonacci, desde Casita!
—Las rutas que llegan a Hilbert y a Gadner desde Casita pasando por Fibonacci —dijo Mati —, miden respectivamente, 595 y 655. Son peores que las de la tabla, tampoco cambiamos nada ahora.
—¡Nos vamos a Gadner! —gritó Sal.
—El bromista… —dijo Ven.
—Muy bien —dijo ella —A Gadner desde Voronoi.
—Desde Gadner —dijo Mati —no podemos llegar a ninguna librería en amarillo, así que no tenemos que cambiar la tabla.
—¿Siguiente? —preguntó Mati teatrera.
—¡Richter! —dijo el gafotas.
—¡El de los terremotos! —añadió su hermano.
—¡A Richter desde Gauss! —puntualizó la pelirroja.
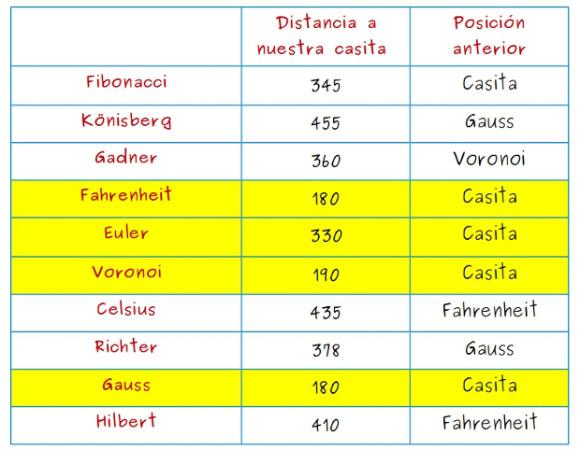
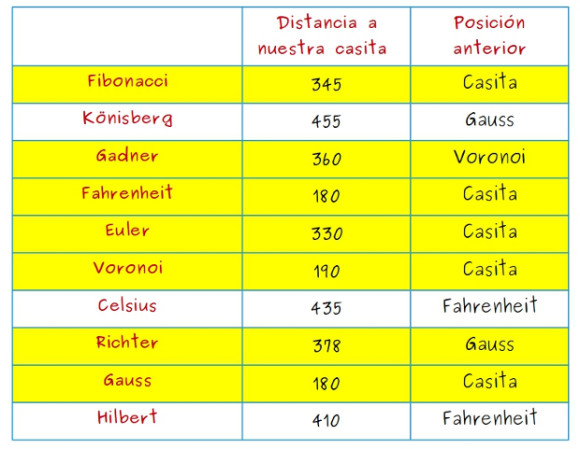
—Tendremos que calcular ahora las rutas que llegan a Könisberg y a Celsius (en amarillo) pasando por Richter —propuso Mati —. Para Könisberg esa ruta mide 603, los 378 de Casita a Richter en nuestro árbol verde más los 225 de Richter a Könisberg; para Celsius, tendemos 658. Los dos son peores que los de la tabla, no cambiamos nada.
—¡Nos vamos a Hilbert desde Fahrenheit! —anunció el gafotas.
—¡Toma! —dijo Ven —¡A ver si nos lleva a su hotel infinito!
—Tampoco tenemos que cambiar la tabla —dijo Mati —porque Celsius está más cerca de Casita si vamos por Fahrenheit.
—¡Vamos que nos vamos! —exclamó el pequeño —¡A Celsius desde Fahrenheit!
—Pues ya está -dijo el gafotas —porque Könisberg está más lejos por Celsius, así que a Könisberg por Gauss como dice la tabla, ¿no, Mati?
—Perfecto —dijo Mati orgullosa de sus exploradores.
-Ya lo tenéis —anunció la pelirroja —Si nos quedamos solo con las aristas verdes, tenemos el árbol que nos proporciona los recorridos de longitud mínima desde casa hasta cualquiera de las librerías que venden nuestro libro.
—¡Toma, toma, toma!¡Mola infinito! —dijo Ven.
—¡Y más allá! —añadió su hermano.
—¡Guauuuuuuuuuu! —dijo Gauss poniendo una nota discordante…











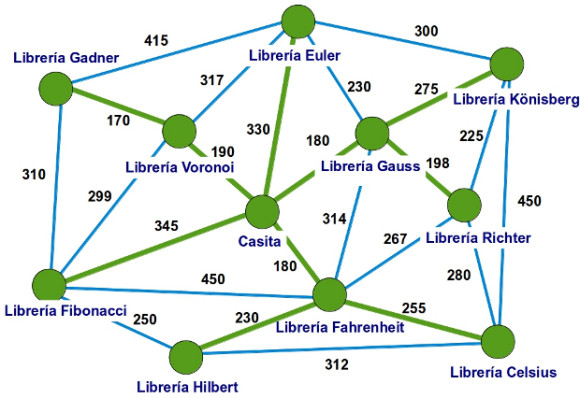

Muy bonito. ¿Hay forma de determinar el camino más largo?. Es que a mi me gusta mucho andar…, además de vez en cuando paro, miro la hora y sea la hora que sea, me digo «¿qué importa la hora?» y entro en el primer bar que encuentro…y me tomo una cerveza con unas gambitas en su sal…¡guau!.
Creo que es Gardner.
utilizar párr Tener ONU T-Mobile Samsung Galaxy S3 4.7 Pulgadas Android 4.1 Teléfono i9300. Sólo con Invitación 99,99 euros! This es mi Primera Vez Que compra en este Sitio, y la Primera Vez Que compra Naciones Unidas Teléfono de marca no. Helo él USADO Durante Una Semana. siguen funcionando bien, flexible toque, Internet de banda ancha, video de Alta Definición, stereo sonido, La Respuesta flexible! Este Teléfono es impresionante! Tiéné Una Cámara de 8MP Una Enorme Pantalla de Alta Definición. Se Cayó dos Veces, Todavia No Hay ningun dano Yo Soy El Mas Agradable con Este acuerdo es el Mejor i9300 Teléfono Que COMPRE ESTA
En la red, que es el precio más bajo! oline en tienda: http://opa.li/4a55
Que facil lo haces.
Carla
http://www.lasbolaschinas.com
Ese gorrión lleva en mi ventana
cantando contento toda la mañana
Hay otro, la hembra, que está en el manzano
y de un corto vuelo se ha ido a su lado.
Este frío invierno mucho habrán sufrido,
porque ha sido mucho lo que aquí ha llovido,
pero entre las nubes el sol ha salido
y de rama en rama se acercan al nido.
Es el infinito algo pequeñito
dos agujeritos en tu naricita
dueña de los vientos, pequeña, bonita
en el firmamento de muchas pequitas.
Este libro, Mati,
muestra tus encantos,
tus preciosos ojos,
tu mejor sonrisa;
es un gran tesoro,
de plata, de oro,
rubí y amatista.
Este mati-libro esconde la magia
de la primavera, pues dijo un poeta
que estaban sus páginas, al igual que ella,
llenas de misterio, bonitos colores,
y su celulosa hecha de madera,
con caolín muy puro, olía cual las flores.
Feliz y orgullosa,
volaba tranquila,
una mariposa,
cuando de repente
quiso ser gitana
y bailar al ritmo
de alguna sardana
y extendió las alas
y al buscar la luna
la encontró en el cielo
detrás de la bruma.
Ese último «poema» (o lo que sea), hecho con todo el cariño, se lo dedico a Raquel, a quien considero una artista de lujo, de mucha categoría. Espero que le guste… y le deseo lo mejor en esta vida suya tan generosa.
beats by dre headphones P . No comment on the quality finish that uses noble materials such as aluminum or leather . As a existing owner of two dre headsets by doctor dre, I can say they deliver fantastic sound and if you can possibly pay for them, then you need to beats by dr dre headphones surely give them an attempt . There could be the 隆掳Studio隆卤 headphones, that action to be an over-the-ear headphone that action to be aimed at flat musicians and about appearance up in audio advance advance videos, for archetype Keri Hilson隆炉s 隆掳Knock You Down隆卤 and Lady Gaga隆炉s 隆掳Poker Face . These dudes have a beats by dre uk ton of energy and talent beats by dre uk that trumpets louder, they also link up with BJ The Chicago Kid while on their ventures . Sound quality is a mixed beats by dr dre bag . Dr . Nipsey隆炉s been doing his thing, Jay Rock had a hit song with Lil Wayne and beats by dre headphones uk will.