—¿Has anotado lo de las patas, Ven?
—Sí, gafotas, he anotado todo –refunfuñó el pequeño –. Pero ¿no deberías apuntar tú algo?
—Yo soy el que está observando, ¿recuerdas?
—Tú eres un carota –protestó Ven –. Si quieres hacer como Calpurnia, deberías anotar tú tus observaciones, ¿no te parece?
—Pero tú escribes más rápido –de defendió Sal –, y si me paro a escribir, se escapa el saltamontes.
—Lo dicho, Sal –sentenció su hermano –, eres un carota.
—¿Qué, chicos? —Mati se acercó a los niños – ¿Escribiendo un cuaderno como el de Calpurnia Tate?
—Eso es, Mati –contestó Sal.
—De eso nada, Sal –protestó Ven –. Yo estoy escribiendo el cuaderno, tú solo estás mirando, mirando y mirando embobado al saltamontes.
—De eso se trata, Ven –dijo el gafotas –. Antes de concluir algo, hay que observar muy bien.
—Pero es que yo también tengo ojos en la cara, ¿sabes? —respondió Ven –. Yo también puedo mirar y observar al saltamontes, pero tú me tienes de sirviente escribiendo todo el rato para no tener que escribir tú…
—Bueno, bueno, bueno –terció Mati –, no nos enfademos, chicos. Se me ocurre una idea: como tenemos papel, lápiz y un saltamontes, os puedo explicar un acertijo matemático muy curioso sobre saltos de saltamontes.
—¿Sí? ¿Cuál? —preguntó el pequeño un poco desconfiado.
—¿Y si se va este saltamontes, Mati? —preguntó Sal.
—No pasa nada –dijo ella –,, buscaremos otros después. ¿Os lo cuento?
—Venga –aceptó el pequeño.
—Se trata de dibujar un línea que tenga longitud natural –les dijo –, es decir, longitud 1, 2, 3, 4… cualquier número natural que queráis. Un saltamontes tiene que dar, sin salir de la línea y empezando por uno de los extremos de la misma (le llamaremos I a ese extremo, de inicio), tantos saltos como indique el número que mide la longitud de la línea. Pero esos saltos irán aumentando su longitud 1 a 1, comenzando con un salto de longitud 1, luego uno de longitud 2, después de longitud 3… y así, sucesivamente, hasta que dé un salto de la longitud total de la línea. Eso sí, los saltos pueden ser hacia adelante o hacia detrás, siempre que no salgan, como hemos dicho antes, de la línea original.
—No entiendo muy bien, Mati –interrumpió Ven.
—Vamos a verlo con un dibujo –propuso la pelirroja –. Si la línea tiene longitud 1, hay que dar solo un salto de longitud 1. Si la línea tiene longitud 2 hay que dar 2 saltos: el primero de longitud 1 y el segundo de longitud 2. Si la línea tiene longitud 3, hay que dar 3 saltos: el primero de longitud 1, el segundo de longitud 2 y el tercero de longitud 3. Y así, sucesivamente. Llamaremos I al punto inicial y F al punto final.
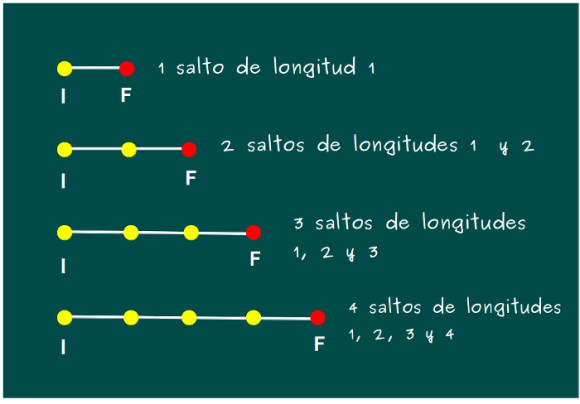
—La pregunta es –continuó ella –: ¿cuándo se puede terminar en el punto F siguiendo esta regla? ¿Para qué valores se consigue?
—Con longitud 1, fácilmente –apostilló Sal.
—Efectivamente –dijo Mati.

—Con 2 no se puede, ¿verdad, Mati? —preguntó el pequeño –Porque no se puede dar el segundo salto, ¿no?
—Eso es, Ven –dijo esta –.Muy bien.

—Y con longitud 3… —comenzó a decir el pequeño –, el primer salto tiene que ser hacia adelante siempre…

–… el segundo salto –continuó Ven –debe ser hacia adelante también…

–… y el tercero –concluyó –tiene que ser, necesariamente, hacia atrás y no termina en F. Pues vaya, no se puede.

—Pero –dijo Sal de pronto muy entusiasmado – ¡con 4 sí que sale! ¿Verdad, Mati?
—Sí, señor –dijo ella –. Porque el primero es hacia adelante, el segundo también, el tercero hacia atrás, llegamos al punto de inicio, y con el salto final, que tiene la longitud de la línea, llegamos a F.

—¡Toma, toma, toma! ¡Cómo mola! —exclamó Ven.
—Es chulísimo, Mati –dijo Sal.
—Ya os dije que era muy entretenido –añadió ella guiñándoles un ojo.
—Vamos a ver con 5 –propuso Ven y se puso manos a la obra.
Al cabo de unos segundos, dijo un poco desilusionado:
—Con 5 tampoco sale, vaya. No se puede dar el último salto.
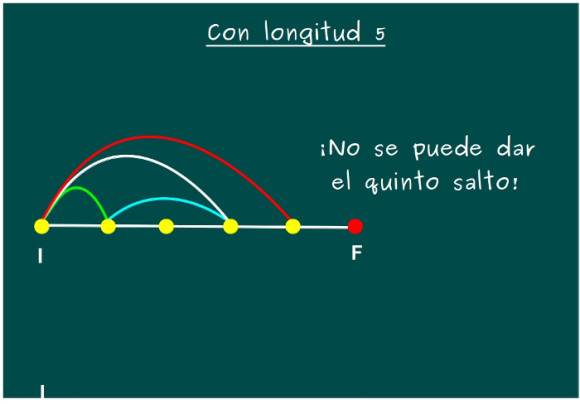
—Os dejo un rato, a ver si encontráis el siguiente número natural para el que el problema tiene solución –les dijo.
Los niños se pusieron manos a la obra. Bueno, en realidad, fue Ven el que pintó las líneas y los saltos, Sal se limitó a dar sugerencias. Gauss estaba persiguiendo al saltamontes por el campo.
—¿Ya no sale hasta el 9, Mati? —preguntó Ven con la cara arrugada.
—Ajá, eso es –confirmó ella.
—O sea –especuló el pequeño –, que solo sale con cuadrados perfectos, ¿no? Como 1 es el cuadrado de 1, 4 es el cuadrado de 2 y 9 es el cuadrado de 3…
—Muy buena observación, Ven –dijo Mati –, pero no, no es esa la regla.
—¿Cuál es el siguiente, entonces? —preguntó Sal.
—Eso os lo voy a dejar como ejercicio a vosotros y a nuestros amigos lectores –respondió Mati –. Esta es nuestra última aventura hasta Septiembre, así que invitamos a nuestros amigos a encontrar todas las soluciones posibles para líneas de hasta 20 unidades de longitud, y que nos lo cuenten en los comentarios de este capítulo.
—¡Mola! —dijo el pequeño y añadió con cara de pillo – Así, si a nosotros no nos salen, se lo copiamos a ellos.
—¿Por qué solo hasta 20, Mati? —preguntó Sal.
—Bueno –dijo ella –porque si no puede ser muy largo, ¿no? Este juego es muy entretenido para que se lo propongáis a vuestra familia o a los amiguitos que conozcáis en las vacaciones.
—¡Vale! —exclamó Ven.
—Y os contaré un secreto, ¿vale? —añadió ella con voz misteriosa –Para 20 y números mayores que 20, me han contado que el problema tiene solución si la longitud de la línea es un número tal que al dividirlo por 4, da como resto 0 o 1.
Los niños se quedaron pensando un instante, Sal dijo de pronto:
—O sea, que con 20 se puede.
—Ajá –dijo Mati.
—Toma, y con 21 –añadió Ven –, porque al dividir 21 entre 4 nos queda de resto 1.
—Eso es –dijo ella.
—Y con 24, y con 25… —siguió el gafotas.
—¡Muy bien! —exclamó la pelirroja –Veo que lo habéis entendido.
—¿Seguimos buscando bichos, Ven? —preguntó Sal.
—Vale –dijo este –, pero ahora escribes tú, ¿eh?
FIN
Pues sí, nos vamos de vacaciones hasta septiembre. Esperamos vuestras respuestas en los comentarios, ¿para qué números entre el 9 y el 19 tiene solución el problema del saltamontes?
Hasta que volvamos a vernos, esperamos que disfrutéis mucho de las vacaciones, que descanséis y ahora que tenéis menos tarea, aprovechad para decirle a la gente que queréis, eso, que las queréis.
Hasta pronto
MATI




