—¡Hemos ganado el Pitágoras, hemos ganado el Pitágoras! —gritaba Ven con los ojos cerrados y sus brazos en alto.

—El Pitágoras no, Ven, el Bitácoras, Bi-tá-co-ras —Sal tampoco podía dejar de sonreír y saludar a todo el mundo que pasaba por la calle.

—¡Que no, que es el Pitágoras, como el de la estrella de 5 puntas! ¡Que Mati es matemática también! ¿A qué sí, Mati?

—Bueno, los dos tenéis razón. Soy matemática y hemos ganado el premio Bitácoras —dijo ella, también sonriendo como si no hubiese mañana.

—¿Y Bitácoras también era un matemático griego, Mati? —preguntó el pequeño.

—No, Ven, no. Una bitácora era el sitio de los barcos donde se guardaba la brújula para protegerla de las inclemencias del tiempo y de las perturbaciones que los hierros del navío pudieran producir sobre el campo magnético de la misma.

<!—more—>—¿¿¿Qué??? —respondió el pequeño, con la nariz arrugada.

— La ‘cajita’ que protegía a la brújula para que siempre apuntara al Norte… —Mati bajó un poco el volumen y concluyó —…magnético.

—¡Ah, magnéticos, como un juego que tenemos en casa para hacer construcciones!

—Más o menos. —concluyó la gafotas.

—¿Y qué tiene que ver eso con los premios Bitácoras, Mati? ¿Por el magnetismo? ¿Por navegar en la red?

—No, no. Es que el cuaderno de navegación, a veces, se guardaba dentro de la bitácoras para protegerlo de la lluvia, el sol, el viento…y se conocía como cuaderno de bitácoras. Actualmente, cuando se habla de bitácoras en internet, estamos hablando de un blog, que es una especie de cuaderno…

—Aaaaaah… —dijeron los dos hermanos al unísono.

—Ha sido tan emocionante, Mati… —el pequeño Ven andaba a saltitos.

— Y ¿cuántos miembros del jurado nos han votado a nosotros? —preguntó Sal

—No lo sé, cielo.

— Pero, ¿cómo votan? ¿Dando puntuaciones del 1 a 10 como en el cole? ¿O diciendo cuál es su favorito?

—Tampoco lo sé. Pero déjame que planteemos un pequeño problema sobre una votación.

—¡Sí! —gritaron el gafotas y su hermano pequeño.

—Imaginemos que en la final de un concurso tenemos tres candidatos. Por ejemplo, en la categoría de lindeza, estáis vosotros dos y Gauss.

—¡Gana Gauss, seguro! —Sal acarició a su mascota

—Puede ser. Pero imaginemos que le piden a los miembros del jurado, 11, como en los Bitácoras, que ordenen a los candidatos según sus preferencias y que obtenemos el siguiente resultado.

Un miembro del jurado entrega esta papeleta

Otros 4 miembros del jurado ésta otra

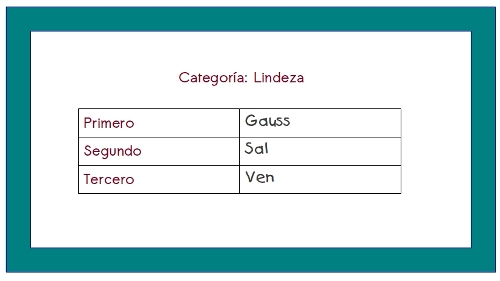
También 4 de ellos la tarjeta

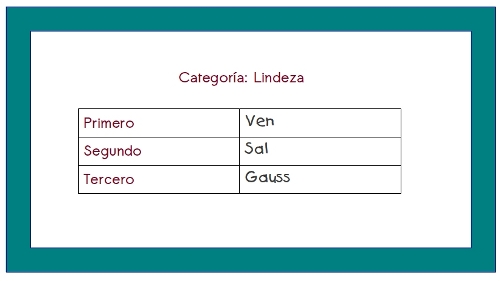
Y 2 de ellos, ésta

Vamos a representarlo en una tabla para verlo mejor. Si elegimos como ganador al que más gente prefiere en primer lugar, éste sería Gauss, con 5 votos, pero seguido de muy cerca por Ven, con 4 votos.

Gauss sonrió pícaramente mientras sus dueños lo miraban con ‘pelusilla’.

—Como no hay mayoría absoluta, es decir, Gauss no es el mejor para más de la mitad del jurado, porque hay 6 personas que no piensan que Gauss es el más lindo, haremos una segunda vuelta eligiendo sólo entre los dos que más gente elige en primer lugar, esto es, sin contar a Sal. Eso se hace en muchas países para elegir a su presidente.

El gafotas arrugó la carilla.

—Sal, es sólo una simulación, cielo. Pues bien —continuó Mati —si, en función de las preferencias del jurado, elegimos sólo entre Gauss y Ven, ganaría Ven con 6 votos, sobre los 5 de Gauss.

Ven sacó la lengua a su mascota con ironía.

—Ahora bien, alguien puede protestar por esto. ¿Por qué elegir entre Gauss y Ven si Gauss está en última posición en la papeleta de 6 de los miembros del jurado? Es el que más veces ‘pierde’ de los 3. Votaremos entre Sal y Ven, y en ese caso, ganaría Sal con 6 votos, mientras que Ven se quedaría con 5.

—¡Qué lío, Mati! —Ven estaba mareado.

—Pues sí, depende a los criterios que quieras atender, hay un ganador diferente. Esto ya lo explicó Arrow en su Teorema de la Imposibilidad. Si hay 3 o más opciones, es imposible diseñar un sistema de votación que cumpla todos esos criterios.

—¿Y si se vota dando puntos? — siguió preguntando Sal.

—En ese caso, también estás ordenando tus preferencias, ¿no?

—Ah, claro.

—Pues sí que es difícil ser jurado, Mati…—apostilló Ven con cara de preocupación.

—Pues sí, Ven, de este tipo de situaciones ya se dio cuenta un señor del siglo XVIII, Nicolas de Condorcet. Es decir, que aunque las preferencias de cada votante es transitiva, el resultado final, puede no serlo.

—¡Transitiva! Eso lo hemos estudiado en la clase de matemáticas. —gritó Sal.

—¿Qué es eso? —preguntó el más pequeño cabizbajo.

—A ver, pensemos en 3 dados, Ven —empezó a decir Mati —Los lanzamos los tres a la vez. Si el primero saca más puntos que el segundo, y el segundo saca más puntos que el tercero, ¿quién ha sacado más puntos el primero o el tercero?

—¡Toma, Mati, el primero!

—Eso es un propiedad transitiva, ¿ves? Si A es mayor que B y B es mayor que C, entonces A es mayor que C.

—Claro, Sal es mayor que yo y yo soy mayor que Elio, entonces Sal es mayor que Elio.

—Exacto. Esto me recuerda a un juego con dados con el que podéis sorprender a papá y mamá, el de los dados no transitivos.

—¿Dados no transitivos? Imposible, Mati. —dijo Sal con la mirada de sospecha.

—A ver, vamos a construir con cartulina, tijeras y pegamento, 3 dados cada uno con la siguiente numeración en sus caras

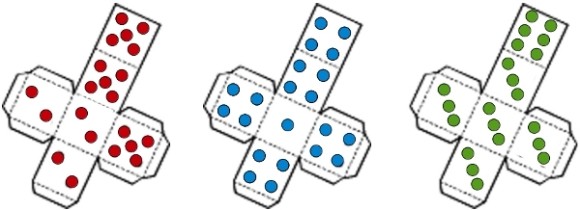
—Están mal, Mati —dijo Ven con cara seria.

—No, no están mal, son diferentes —la pelirroja guiñó un ojo — Vamos a proponer el siguiente juego a nuestro adversario. Le diremos que elija un dado, el que quiera. Nosotros elegiremos otro, después, y ganará el que más veces haya ganado después de 10 lanzamientos, ¿vale? Si dicen que estos dados están ‘mal’, le diremos que, bueno, que todas las caras suman 21 en los tres dados y que por lo tanto, la media de la puntuación de cada tirada es 21/6 en todos y que todos tienen las mismas posibilidades de ganar. Si el contrincante no lo piensa mucho, pensará que es verdad.

—¿No lo es, Mati? —preguntó el gafotas con cara de pillo.

—No, no lo es. Si usamos el rojo y el azul, vamos a ver qué cuantas veces gana el rojo y cuántas el azul.

 

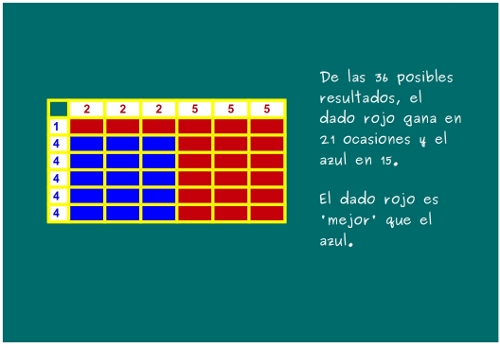
—Ahora, con el rojo y el verde.

—Y por último, el azul con el verde

—O sea que tenemos

—Así, una vez que el contrincante haya elegido su dado, nosotros elegimos en función de esto que sabemos y que no le diremos —y les sonrió con una sonrisa un pelín descarada.

—¡Toma, toma, toma! ¡Cómo mola, Mati! —Ven tenía los ojos abiertos de par en par.

—Me recuerda al juego de piedra-papel-tijera —continuó el gafotas —La piedra gana a la tijera, la tijera gana al papel y el papel gana a la piedra.

—Muy bien, Sal. Ése es otro ejemplo de no transitividad.

—¿Nos vamos ya? Quiero contarle a todos mis amigos que ¡nos han puesto un 10!