—¡¡Y que cumplas muuuuuuchos más!! ¡¡Bieeeeeeen!! —Todos los amiguitos de Sal, cantaban con alegría para felicitarlo por su noveno cumpleaños, pero sobre todo Ven y Elio.

—¡Ya tienes casi 10 años, Sal! —Elio miraba a su primo con admiración, como a un ídolo.

—Bueno, bueno, Elio, me falta un año completo.

—Pero 9 es casi 10, eso sí —dijo Ven orgulloso de su hermano, con una sonrisa de oreja a oreja mientras acariciaba el nuevo balón de fútbol que le habían regalado a Sal.

—Si tuviera 9’9999999999…. años, entonces si que tendría casi 10, ¿eh chicos? —repuso el gafotas con una sonrisa.

—Pero para que tengas 9’9999999999….con infinitos nueves, falta exactamente un año, porque 9’9999999… con infinitos nueves, que se dice 9’9 periodo, es exactamente 10. ¡Feliz cumpleaños, Sal!

Era Mati la que acababa de entrar en el salón para no perderse la tarta de galletas y chocolate habitual en los cumpleaños de la familia.

—¡Hola Mati! —Ven soltó el balón y se abrazó la pelirroja, Gauss movió la cola con alegría y se unió al abrazo.

—¿Me habéis guardado un poco de tarta?

—Claro, Mati —Sal se acercó a ella, feliz, pero ya con la mirada de sospecha —No puede ser, Mati, 9’99999999999… no es 10, le falta un poco, ¿verdad?

—No, no le falta nada. En nuestro sistema de numeración, el decimal, 9’99999….. es 10, es otra forma de escribirlo, simplemente. Como 0’9999999999999… es 1.

—No te creo, Mati… ¿Es una broma?

—No, cielo, no es una broma.

Ven y Elio miran con los ojos como platos a Mati esperando la magia de la pelirroja. En ese momento, ella saca su pizarra.

—Vamos a verlo, chicos. Para ello, primero dividimos 1 entre 9.

—Ya tenemos que 1/9=0’1111…

—Ahora si multiplicamos por 9, tenemos:

—¡Toma, toma, toma! —el pequeño Ven alucinaba y saltaba abrazado a Elio.

—En realidad, son sólo 2 formas distintas de nombrar al mismo número —remató la gafotas.

—Es increíble, Mati, me gusta tener 9 años, ¡me gusta el 9! —Sal estaba emocionado y deseando llegar al cole para contárselo a sus compañeros.

—Pues te voy a regalar otro truco del 9 para que se lo enseñes a tus amiguitos. Se llama la prueba del 9 y sirve para saber si hemos hecho bien, por ejemplo, una multiplicación. Pero antes necesitamos saber qué es la raíz digital de un número.

—¿Cómo la raíz cuadrada? —preguntó Ven al que le sonaba de algo.

—No, mucho más fácil, Ven. Para calcular la raíz digital de un número, sólo hay que sumar sus cifras. Si el resultado tiene más de una cifra, lo volvemos a sumar. Y así hasta que nos quede una sola cifra. Vamos a hacer un ejemplo.

—Pues, muy bien —continuó Mati— si tenemos una multiplicación, por ejemplo… A ver, ¿quién me dice una?

—9654 × 48 —se apresuró a decir Ven con cara de pillín.

—Estupendo, ¿la haces, Sal?

El gafotas se puso con empeño en la pizarra, y al cabo de un rato, con su hermano y su primo admirando su tarea, tenía en la pizarra

—Muy bien, pues ahora pintamos una equis y ponemos en la parte de arriba de la equis la raíz digital del factor de arriba y en la parte de abajo, la raíz digital del factor de abajo, así

—A continuación, multiplicamos los dos números que están en la equis, calculamos su raíz digital de nuevo y lo colocamos a la derecha.

—Pues bien, la raíz digital de nuestro resultado, 463392, debe ser 9, porque si no, está mal hecha la operación.

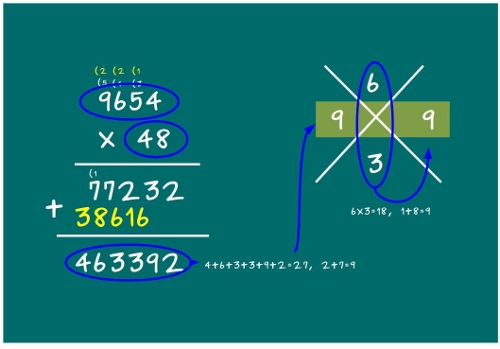—¡Soy un crack! —exclamó Sal al ver que la raíz digital de su producto coincidía con la raíz del producto de las raíces digitales —¡Oé, oé, oé…!

Ven y Elio se unieron a la fiesta y los tres bailaban en círculos alrededor de Gauss que empezaba a marearse.

—Efectivamente, tu resultado está bien, pero, ¿y si hubieras escrito 643392, sólo intercambiando las 2 primeras cifras?

Sal dejó de bailar, los otros dos siguieron un poco más.

—Pues que la raíz digital del resultado también sería 9 y sin embargo, la cuenta está mal hecha…—contestó el gafotas perdiendo poco a poco el entusiasmo y bajando progresivamente la voz.

—Sí, la prueba del 9 sólo es definitiva para afirmar que te has equivocado. Pero puede dar falsos positivos.

—Entonces, ¿por qué se usa, Mati?

—Bueno, principalmente, porque la probabilidad de obtener un falso positivo es relativamente baja, es decir, que casi siempre acierta.

En ese momento, Ven dejó de bailar y exclamó:

—¡Toma, además 9 son los planetas de nuestro sistema solar!

—No, son 8 y lo sabes, Ven, Plutón no es un planeta —le contestó su hermano con cierto aire de cansancio.

—Para mí, sí es un planeta, es mi favorito y tengo un planetario chulísimo que tiene a Plutón.

El pequeño siempre se enojaba con este asunto.

—Pero porque es antiguo, Ven, los nuevos no lo traen.

—Sal tiene razón, Plutón ya no es un planeta, desde 2006…

—¡El año que yo nací! —interrumpió Elio.

—Exacto, Elio, en 2006, cambiaron la definición de planeta y Plutón pasó a ser un planeta enano.

—No me importa, a mí me gusta, y es un planeta —la carita de Ven se ensombreció de tristeza.

—A mí también me gusta, Ven —siguió Mati —pero como Plutón hay más objetos similares, incluso más grandes, como Eris. Además, su órbita, la de Plutón, es diferente a la de los otro ocho planetas, no es circular y está más inclinada…

—A mí tampoco me importa —bufó Elio con cara de enfadado —Es el más pequeñito y no lo podemos dejar solito…

—Pero no está solito, chicos, tiene, al menos, cuatro lunas que lo acompañan, ¡más que la Tierra! En cualquier caso, chicos, no nos pongamos tristes, que es el cumpleaños de Sal. Por cierto, mira lo que hay por aquí…

Mati sacó una bolsa de colores y se la entregó a Sal que la abrió con alegría y sacó ¡otro balón de fútbol!

—¡Ya te han regalado dos balones, Sal! —dijo Ven con alegría.

—¡Me encanta! —dijo el gafotas —A éste le llamaremos “Plutón” y será nuestro balón de la suerte. Vamos a probarlo.

Pues sí, la prueba del 9 sirve para detectar si nos hemos equivocado al hacer una multiplicación. Para que la multiplicación esté bien, el producto de las raíces digitales de los factores debe coincidir con la raíz digital del producto

Pero también se puede usar, de forma similar, para comprobar sumas, sabiendo que la suma de las raíces digitales de los sumandos debe coincidir con la raíz digital de la suma

O, si se quiere, para la división, como vemos en el siguiente ejemplo

Pero no hay que confiar si el resultado es positivo, porque al alterar el orden de dos de las cifras del resultado de cualquiera de estas operaciones, la raíz digital de dicho resultado. En cualquier caso, como la probabilidad de que nos hayamos equivocado exactamente en dos números cambiados de sitio, en la mayoría de los casos funciona. Eso sí, si la prueba dice que lo hemos hecho mal, seguro que lo hemos hecho mal.

En latín, a esta prueba se le llamaba Abjectio novenaria y ya era conocida por el obispo Hipólito en el siglo III y usada en el XII por matemáticos hindúes. En cuanto a los falsos positivos, ni siquiera Richard Buckminster Fuller se dio cuenta cuando la usaba, ¡y eso que Fuller era un señor muy listo que fue muy famoso gracias a la tensegridad!

En todo caso estas pruebas se basan en que si

p x q = s entonces p(mod 9) x q (mod 9)= s(mod 9)sabiendo que p (mod 9) es el resto de dividir p por 9Por tanto si la segunda igualdad no se da, podemos afirmar que la primera también es falsa. Sin embargo, si se da la segunda igualdad no podemos afirmar con un 100% de garantía que la cuenta esté bien realizada.

Entonces surge la pregunta ¿por qué módulo 9?

Es evidente que para este tipo de comprobación necesitamos un número que verifique dos condiciones:

1. El cambio de cualquier dígito del número ha de influir sobre la divisibilidad: esto por ejemplo no ocurre con el 2 o el 5 (en los que la divisibilidad de un número sólo depende del último dígito), ni con el 4 (la divisibilidad depende de los dos últimos dígitos), ni con el 8.

2. Debe ser fácil de comprobar la divisibilidad por dicho número.

Estas dos condiciones nos limitan al 3, 6 y 9, pero la prueba tal y como la hemos descrito es la más adecuada porque para obtener un falso positivo hay que equivocarse en más de un dígito.

Si queréis profundizar más sobre cómo Plutón dejó de ser un planeta para ser un plutoide, os dejo este enlace y un vídeo muy divertido sobre el caso Plutón.