—A lo mejor nos encontramos un día por Madrid…
—¿En serio, Sal? —preguntó Verónica ilusionada —¿Vais a ir a Madrid?
—Sí —contestó el pequeño Ven con un hilillo de voz —Mati nos ha dicho que nos va a llevar a ver el Museo del Prado…
—Para ver Las Meninas, claro… —dijo Verónica.
—Sí —confirmó el gafotas —Y también un relieve que le gusta mucho a Mati, «Las Ciencias Matemáticas«:http://www.museodelprado.es/coleccion/galeria-on-line/galeria-on-line/obra/las-ciencias-matematicas/, creo que se llama.
—Eso —añadió Ven —Es que se parece un poco a nuestra Mati, porque las Matemáticas están representadas con una figura de mujer y hay algunos niños a su alrededor como nosotros…y hasta tiene un perrito, como nuestro Gauss.
De pronto los tres niños se quedaron callados. Sal se miraba las sandalias como si nunca antes las hubiese visto, Ven apretaba fuerte los labios para que no le temblase la barbilla, Verónica miraba al mar como si esperase encontrar algún día más de vacaciones, Gauss… Gauss estaba más triste que ninguno de los niños. Nuestros tres amigos habían pasado unos días muy emocionantes desde que conocieron a Verónica una mañana en la playa, era la chica más divertida que jamás habían conocido y tiraba unos puñados de arena impresionantes a pesar de su mano pequeñita. Era la última tarde que estaban juntos porque ella volvía con su familia a Madrid.
—¿Jugamos a algo? —preguntó la niña.
—Me duele un poco la tripa —se excusó Sal arrugando su nariz para subir sus gafotas.
—Si fuésemos piratas nos podríamos escapar en nuestro barco y no volver al cole —dijo Ven con sonrisa pícara.
—Guau —los ojos de Verónica brillaron de repente —Podríamos ir a América, y ver las ruinas del imperio maya…
—Huy, no —interrumpió Ven —Ésos me dan mucho yuyu con lo del fin del mundo y tal…
—¡Eso son tonterías, Ven! —replicó Sal —No estás siendo nada científico.
—¿Creéis que podríamos llegar nadando hasta el horizonte? —preguntó Verónica que parecía absorta en sus pensamientos aventureros y no escuchaba la discusión entre los hermanos, mientras Gauss la miraba embobado.
—Verónica —dijo Sal muy serio —Nunca se puede llegar hasta el horizonte, el horizonte se mueve…
—¡Qué guapos estáis mirando al mar! Me recordáis una canción de Jorge Sepúlveda…
—Hola, Mati —dijeron los tres al unísono.
—Mati —preguntó Verónica inmediatamente —¿tú crees que se puede llegar al horizonte nadando?
—Que no, Verónica —protestó sin mucho interés Sal —que el horizonte se mueve, no se puede alcanzar…
—En eso tiene razón, Sal —dijo Mati —Pero si que podemos, si os apetece, calcular la distancia desde aquí hasta el horizonte que vemos desde aquí.
—¡Toma! —se animó Ven —¡Venga!
—¡Sí, sí, sí! —a la nueva amiga de Sal y Ven le apasionaban las mates.
—¿Os acordáis del Teorema de Pitágoras? —les preguntó la pelirroja.
—Claro —respondió el pequeño —Nos lo explicaste cuando nos enseñaste las «coordenadas cartesianas«:http://blogs.20minutos.es/mati-una-profesora-muy-particular/2012/03/28/descartes-y-los-barquitos/les
—¿Ése es el de los catetos? —preguntó divertida Verónica.
—Efectivamente —corroboró Mati —En un triángulo rectángulo, es decir, un triángulo con una ángulo recto…
—Como el de la esquina de una portería… —añadío Ven.
—Eso es —continuó la gafotas —Pues en un triángulo rectángulo, si llamamos catetos a los lados que forman el ángulo recto e hipotenusa al lado que falta, el teorema de Pitágoras nos asegura que el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de los catetos.
—¡Ya, ya! —gritó Verónica —¡Cateto al cuadrado más cateto al cuadrado es igual a la hipotenusa al cuadrado!
—Muy bien —la felicitó Mati.

—¿Quieres ser matemática, Verónica? —preguntó Sal curioso.
—No, quiero ser médica, pero me encantan las mates.
—¿Seguimos? —preguntó Ven con impaciencia.
—Sí, seguimos —dijo Mati —Vamos a fijarnos en el siguiente esquema. Pintamos los radios de la Tierra, uno el que nos uniría a nosotros con el centro de la misma, y otro a un punto del horizonte. En verde dibujamos nuestra altura sobre el nivel del mar, y en amarillo la distancia hasta ese punto del horizonte. Pues bien, lo importante es darse cuenta de que la línea amarilla y el radio de la Tierra correspondiente en el punto del horizonte forman un ángulo recto.

—¿Cómo lo sabes, Mati? —preguntó Sal impaciente.
—Pues porque la línea amarilla es tangente a la circunferencia en ese punto y eso sólo es posible si el ángulo que forma con el radio en dicho punto es un ángulo recto.
—Vale, es recto, ¿y ahora qué? —Verónica estaba impaciente por conocer la distancia al horizonte.
—Pues, que tenemos un triángulo rectángulo —respondió Mati —y podemos usar el teorema de nuestro amigo Pitágoras. Vamos a fijarnos sólo en el triángulo. Como medida del radio de la Tierra tomamos el valor medio de su radio, 6371 kilómetros…
—¡Hala! —interrumpió Ven.
—…y suponemos que estamos a una altura de 10 metros sobre el nivel del mar porque estamos en el paseo marítimo —terminó de decir la gafotas.
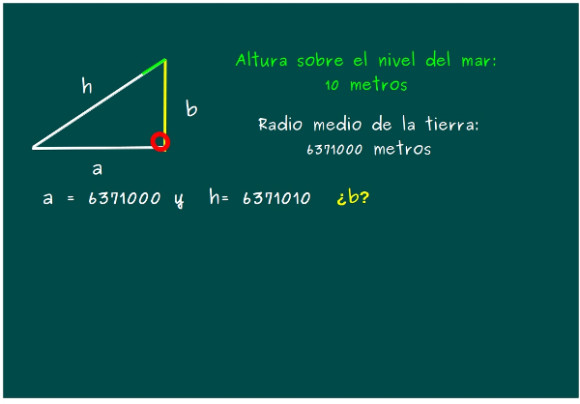
—¡Claro! ¡Si conocemos dos lados del triángulo rectángulo, podemos conocer el tercero, como nos explicaste aquella vez!
—Efectivamente, Sal —dijo la pelirroja orgullosa — Como queremos conocer la longitud del cateto b, lo despejamos de la fórmula de Pitágoras.

—Ahora sólo tenemos que sustituir a y h por su valor para tener el valor de b —les dijo.

—Pero, Mati —observó Sal —Lo que nos da es el valor de b al cuadrado…
—Bueno —contestó ésta —sólo tendremos que calcular la raíz cuadrada de 127420100…
—Yo no sé hacer eso —dijo Verónica con penita.
—Pero Mati te puede enseñar —respondió Ven con entusiasmo — A nosotros nos enseñó un «método muy sencillo para hacerlo«:http://blogs.20minutos.es/mati-una-profesora-muy-particular/2012/04/11/esa-raices-tan-cuadradas/, ¿verdad, Mati?
—Claro que se lo enseñaremos a Verónica —dijo Mati —pero después, ahora vamos a usar la calculadora para poder darnos un baño antes del almuerzo.

—¡Toma, toma, toma! ¡Más de 11 kilómetros! —Ven estaba entusiamado —¡Tú no puedes nadar eso, Verónica!
—¡Ni tú! —contestó la niña un poco enfurruñada.
—No, ni yo —dijo Ven —No te enfades que es nuestro último día…
Un silencio se apoderó de la escena y la cara de los niños se ensombreció. Gauss agachó su morro.
—¿Y sabéis qué? —trató de animarlos Mati —¿Veis aquel mástil de un barco a lo lejos?
Los tres niños asintieron con sus cabecitas.
—¿Queréis saber a qué distancia está es barco?
—¿¿Cómo?? —preguntó el gafotas intrigado.
—Lo vais a saber enseguida… —anunció Mati con voz misteriosa —Tendríamos que saber cuánto mide el mástil… Pero si mide 10 metros que es exactamente nuestra altura sobre el nivel del mar, y os fijáis en el siguiente dibujo…

—¡Toma, toma, toma! —gritó Verónica saltando sobre la punta de sus pies —El doble de distancia que desde aquí al horizonte, ¿no, Mati?
—Eso es —corroboró ella.
—Más de 22 kilómetros… —murmuró Sal pensativo.
—Aproximadamente —Mati le alborotó el pelo y sal se sonrojó, posiblemente quería parecer más mayor delante de su amiguita.
—¿Y si no mide 10 metros el mástil? —preguntó Ven desconfiado.
—En ese caso, mira —dijo Mati mientras dibujaba un nuevo esquema en la pizarra.
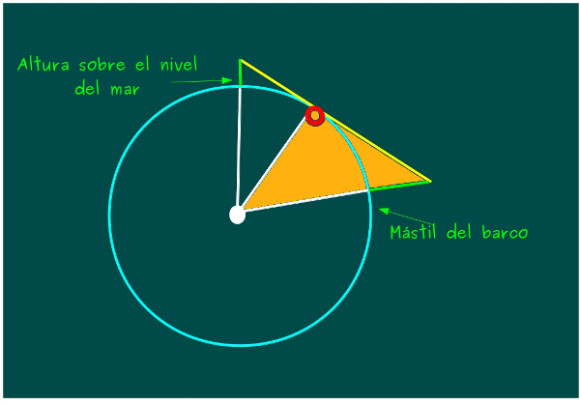
—Como conocemos la distancia desde nosotros hasta el horizonte —les contó —sólo queda calcular la distancia desde el punto en el horizonte hasta el mástil, pero eso lo podemos resolver de nuevo usando el teorema de Pitágoras en el triángulo naranja.
—Es maravilloso, Mati —Sal estaba alucinando con lo que les contaba Mati.
—Ojalá fuera nuestro barco —dio de pronto Verónica con los ojos brillantes —Yo sería la capitana y podríamos ir a América.
—¿Sin mayores? —preguntó Ven un poco angustiado.
—¡Sin mayores! —respondió ella con gesto firme y decidido —Iríamos a ver las ruinas mayas…
—¡Yo voy contigo! —dijo inmediatamente Sal pero cuando Verónica se volvió hacía él para mirarlo, éste le preguntó, un pelín sofocado, a Mati —¿A qué distancia más o menos está América, Mati?
—Podríamos decir que a unos 6000 kilómetros… —le contestó.
—¡Hala! 6000 kilómetros en barco… —Ven estaba un poco nervioso —y sin mayores… Yo no voy, me quedo cuidando de Gauss.
—Sí, es un largo viaje para hacerlo vosotros solos —corroboró la gafotas —pero os hago una pregunta, ¿hasta que altura tendríamos que subir en globo para poder divisar América desde aquí?
Los niños se quedaron pensando muy serios…
—No me digas, Mati —dijo Sal —¿otra vez el teorema de Pitágoras?
—¡Ajá! —respondió ella guiñando un ojo mientras hacía un nuevo dibujo en su pizarra.

—Pues nada, chicos —les animó Mati —ya sólo necesitamos hacer las cuentas…
Los tres niños se pusieron manos a la obra con la ayuda (muy poquita ¿eh?) de Mati.

—¡Toma, toma, toma! ¡Cómo mola! —Ven se abrazó con fuerzas a Verónica de la emoción. Sal también, posiblemente también emocionado —Más de 2300 kilómetros…
—Aproximadamente, sí —dijo Mati —Si subimos a esa altura y las condiciones meteorológicas lo permitiesen, podríamos ver América.
—Pero eso es altísimo… —Ven se venía abajo de nuevo.
—Sí, es verdad —añadió Verónica —Será mejor que vayamos en un avión…
—¿Se lo pedimos a nuestras familias para el verano que viene? —dijo Sal alegre.
—El verano que viene… —respondió la niña con los ojos húmedos.
—Ya veremos qué hacemos el verano que viene —interrumpió Mati —Ahora yo os propongo un juego: al primero que llegue corriendo al quiosco, le invito a un helado.
—¿Y a los otros dos? —preguntó Ven.
—También —respondió la pelirroja con un guiño y los tres niños salieron corriendo mientras Gauss se quedaba allí, pensativo…




